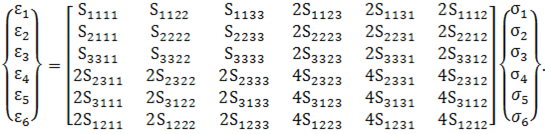Die Voigtsche Notation ist eine verkürzte Schreibweise für Tensoren. Dabei werden jeweils zwei Indizes aus der Tensornotation zu einem Index zusammengefasst. Der neue Index wird auch als Superindex bezeichnet. Das Zusammenfassen der Indizes erfolgt dabei durch folgende Konvention:
.
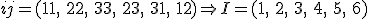Somit kann z.B. der Spannungstensor in einen Spaltenvektor umgewandelt werden:
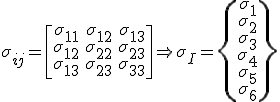
Die ersten drei Komponenten werden auch als Normal- und die letzten drei Komponenten als Schubspannungskomponenten bezeichnet. Voraussetzung für diese Umwandlung ist die Symmetrie des Spannungstensors.
Auch der Verzerrungstensor kann mit der Superindexschreibweise dargestellt werden:
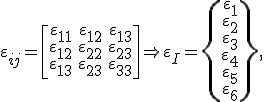
wobei hier zu beachten ist, dass
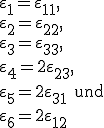
gilt.
Hier entsprechen ebenfalls die ersten drei Komponenten den Normal- und die letzten drei Komponenten den Scherkomponenten.
Besonders beim Umschreiben des Verzerrungstensor von der Vektor auf die Superindexschreibweise ist auf auf den Faktor 2 zu achten.
Dieser findet seinen Ursprung bei dem Umschreiben des Werkstoffgesetzes in die Superindexschreibeweise:
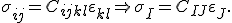
Es soll nun die Komponente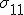 
exemplarisch berechnet werden:
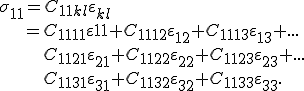
Aufgrund der Symmetrie des Steifigkeitstensors, die unter dem Unterkapitel "Das Werkstoffgesetz" gezeigt wurde, sind einige Einträge dieser Gleichung gleich und können somit zusammengefasst werden:
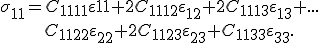(1)
Schreibt man das Werkstoffgesetz in der Superindexschreibweise um, so erhält man:
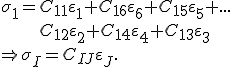(2)
Da sich die Steifigkeitstensoreinträge beim Umschreiben in die Voigtsche Notation nicht ändern sollen wird der vorhandene Faktor 2 in dem Verzerrungsvektor berücksichtigt. Bei der inversen Betrachtung des Werkstoffgesetzes wird dieser Faktor hingegen in der Nachgiebigkeitsmatrix berücksichtigt. Um dies näher zu erläutern, wird die erste Zeile des invertierten Werkstoffgesetzes in der konventionellen und der Superindexschreibweise expandiert, wobei die Symmetrie der Nachgiebigkeitsmatrix und des Spannungstensors verwendet werden:
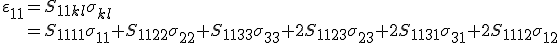
und
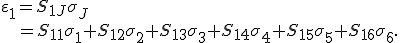
Der Koeffizientenvergleich liefert:
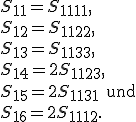
Somit lautet das inverse Werkstoffgesetz:
