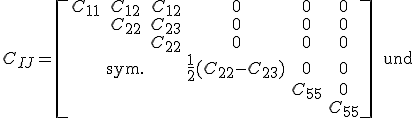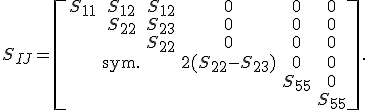Es handelt sich um ein transversal-isotropes Material, wenn zusätzlich zur Orthotropie eine Rotationssymmetrie bezüglich einer Achse vorliegt. Dieses Materialverhalten liegt beispielsweise bei unidirektionalen Einzelschichten vor. Bei transversal-isotropen Materialien können die Einträge der Steifigkeitsmatrix ausgehend von der Steifigkeitsmatrix des orthotropen Materials reduziert werden. Dafür wird eine Drehmatrix aufgestellt, die eine Rotation um die x1-Achse abbildet.
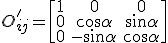
Jetzt wird beispielhaft der Eintrag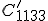 
der transformierten Steifigkeitsmatrix berechnet:
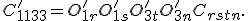
Diese Beziehung wird nun über die Indizes r und s expandiert. Dabei wird sofort verwendet, das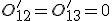 
gilt.
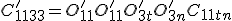
Nun wird zuerst über den Index t und dann über n expandiert. Auch hierbei wird der Eintrag O'31 gleich Null sind.
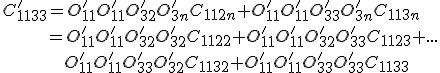
Nun werden die Einträge der Transformationsmatrix eingesetzt:
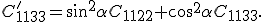
Diese Gleichung wird nun für exemplarische Winkel ausgewertet. Dafür wird zunächst der Winkel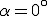 
gewählt. Für diesen Winkel erhält man den folgenden Zusammenhang zwischen den Einträgen der Steifigkeitsmatrix des transformierten und des Ausgangpunkt:
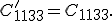
Wird die obere Gleichung für den Winkel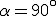 
ausgewertet, erhält man den folgenden Zusammenhang:
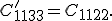
Da die Einträge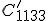 
bei den Auswertungen mit den beiden Winkeln gleich ist (dieser gilt für den identischen transformierten Punkt 
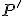), muss somit auch
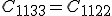
gelten. In der Superindexschreibweise geschrieben heißt das:
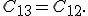
In der analogen Vorgehensweise kann gezeigt werden das
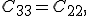
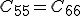und
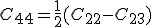
gilt.
Somit reduziert sich die Anzahl der Einträge der Steifigkeitsmatrix für ein transversal-isotropes Material auf 5 unabhängige Einträge.
Die Steifigkeits- und Nachgiebigkeitsmatrix lautet somit:
