Für die Bestimmung der effektiven Ingenieurskonstanten in Faserlängsrichtung wird das Faser-Matrix-System zunächst idealisiert und anschließend homogenisiert. Die Belastung eines Faser-Matrix-Elements in faserparallele Richtung kann als parallelgeschaltete Federn verstanden werden. Die zwei Federn, die die Matrix und die Fasern darstellen, können im Zuge einer Homogenisierung als eine Feder mit der gesuchten effektiven Steifigkeit in Faserlängsrichtung zusammengefasst werden.
Bild: Veranschaulichung des Vorgehens für die Berechnung der effektiven Ingenieurskonstanten in Faserlängsrichtung.
Für die beiden Ersatzmodelle (mit zwei und mit einer Feder) wird nun das "mechanische Kochrezept" angewendet:
- es werden die Gleichgewichtsbedingungen,
- kinematische Bedingungen und
- das Werkstoffgesetz aufgestellt.
Mit diesem Vorgehen können viele elastostatische Probleme gelöst werden. Daher wird im weiteren Verlauf regelmäßig zur Herleitung der Gleichungen darauf zurück gegriffen.
1. Gleichgewichtsbedingung
Es wird ein Kräftegleichgewicht in axialer Richtung aufgestellt. Dafür gilt, dass die aufgebrachte Kraft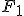 
gleich der Summe der resultierende Kräfte in der Faser 
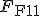und in der Matrix 
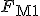ist.
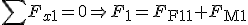(1)
2. Kinematik
Bei der Parallelschaltung von Federn ist deren Auslenkung identisch:
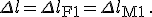
Für die Berechnung der Verzerrungen muss durch die Ursprungslänge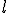 
geteilt werden.
(2)
3. Werkstoffgesetz
Das Werkstoffgesetz für den eindimensionalen Fall (Hooke'sches Gesetz) wird für das homogenisierte System, für die Faser und für die Matrix augestellt.
| homogenisiertes Gesamtsystem: |  |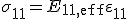
(3) |
| Faser: |  |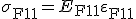
(4) |
| Matrix: |  |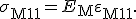
(5) |
Die Gleichgewichtsbedingung (Gleichung (1)) kann in Abhängigkeit der Spannungen geschrieben werden:
(6)
Wird Gleichung (6) durch die Gesamtquerschnittsfläche 
dividiert ergeben sich die Spannung in Abhängigkeit vom relativen Faservolumenanteil:
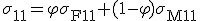. (7)
In die Gleichung (7) wird nun das Werkstoffgesetz für die Faser (4) und für die Matrix (5) eingesetzt:
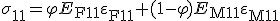. (8)
Aus der Kinematik (2) wird deutlich, dass die Verzerrungen für die Einzelkomponenten der Gesamtdehnung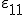 
entsprechen. Somit kann diese in Gleichung (8) eingesetzt und ausgeklammert werden:
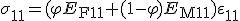. (9)
Der Vergleich der Gleichung (9) mit dem Hookeschen Gesetz (3) ergibt das effektive E-Modul in Faserrichtung:
(10)
Das Vorgehen für die effektive Querkontraktionszahl ist analog und liefert:
(11)