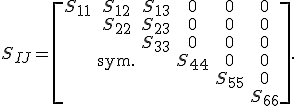Bei einem orthotropen Material liegt eine Materialsymmetrie bzgl. zwei (und somit auch bzgl. drei) senkrecht aufeinander stehender Ebenen vor. Ausgehend vom monoklinen Material wird zusätzlich die (x2-x3)-Ebene herangezogen.
Hierfür ergibt sich folgende Transformationsmatrix:
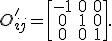
Mit Hilfe des Schema können hier die Steifigkeitseinträge mit ungerader Anzahl des tensoriellen Indexwertes 1 zu null gesetzt werden. Die Steifigkeitsmatrix eines orthotropen Materials besitzt somit 9 unabhängige Einträge.

Die Nachgiebigkeitsmatrix lautet: