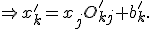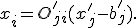Voraussetzung für eine Transformation sind folgende Punkte:
- physikalischer Raum
, - betrachtet werden geradlinige Koordinatenachsen und
- verwendet werden kartesische Koordinatensysteme bzw. orthonormale Basisvektoren.
Orthonormalität bedeutet dabei, dass das Skalarprodukt von zwei verschiedenen Basisvektoren Null und von zwei gleichen Basisvektoren Eins ergibt. Dieser Zusammenhang lässt sich mit dem Kronecker-Delta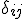 
darstellen.
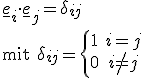
Es soll noch eine kurze Erinnerung an das Skalarprodukt gegeben werden. Dieses ist für zwei Vektoren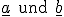 
definiert durch:
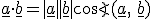
Das Skalarprodukt mit einem Einheitsvektor kann als senkrechte Projektion eines Vektors auf den entsprechenden Einheitsvektor verstanden werden, wie es in der unteren Abbildung dargestellt ist.
Bild: Senkrechte Projektion.
Die euklidischen Transformation ist auch als allgemeine Beobachtertransformation bekannt. Jeder Punkt P im Raum besitzt bezüglich eines Koordinatensystems (z.B. x1-x2-x3-System) einen Ortsvektor. Verändert sich der Beobachtungspunkt in Form des Koordinatenursprungs mit einer Translation und Rotation (z.B. x'1-x'2-x'3-System), lässt sich der Ortsvektor im "neuen" System über den Ortsvektor im "alten" System und eine Drehmatrix bestimmen.
Bild: Euklidische Transformation.
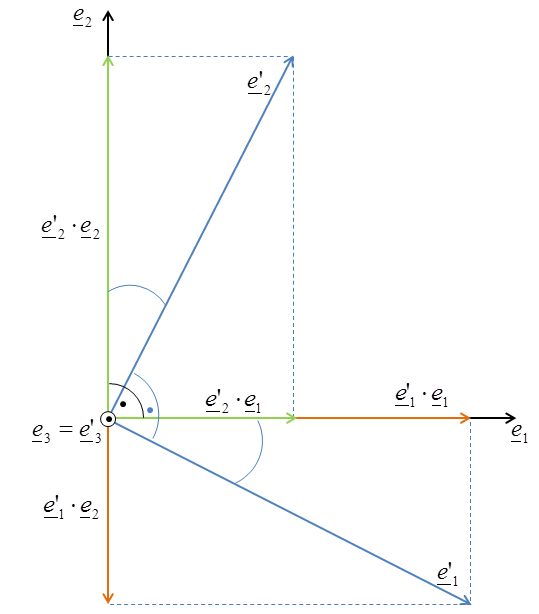
Bei der Drehmatrix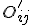 
handelt es sich dabei um eine orthonormale Transformation, die die neuen Basisvektoren 
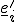auf die alten Basisvektoren 
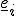abbildet. Die Definition der Drehmatrix lautet somit:
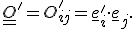
Die Drehmatrix entspricht somit dem Skalarprodukt vom neuen mit dem alten Basisvektor.
Es soll nun der Ortsvektor des beliebigen Punktes P transformiert werden. Zunächst soll dabei vom ungestrichenem "alten" Basissystem in das gestrichene "neue" System transformiert werden.
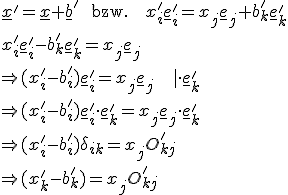
Für die Umrechnung vom gestrichenem "neuem" Basissystem auf das "alte" System ist das Vorgehen analog:
Zur besseren Veranschaulichung der Transformation sollen nun zwei Beispiele berechnet werden. Dies wird an den Beispielen Spiegelung und Drehung gezeigt.
Die Transformationen werden im Anschluss dafür benötigt um die Einträge der Steifigkeitsmatrix aufgrund von Symmetriebedingungen im Material zu reduzieren.