Ein Material heißt monoklin, wenn sich die Materialeigenschaften symmetrisch bezüglich einer Ebene verhalten. Für die Reduzierung der Steifigkeitsmatrixeinträge wird willkürlich die (x1-x2)-Ebene als Symmetrieebene gewählt. Dies ist in der unteren Abbildung für einen exemplarischen Punkt P dargestellt.
Bild: Exemplarische Darstellung von monoklinem Materialverhalten.
Bei der Spiegelung an der Symmetrieebene tritt keine Veränderung des Materialverhaltens auf. Das Materialverhalten ist also invariant bei dieser Transformation in Form einer Spiegelung. Die Transformationsmatrix für diese Spiegelung lautet somit:
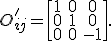
Die Materialsymmetrie fordert nun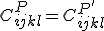 
. Mit Hilfe von Transformationsbeziehungen lässt sich die Steifigkeitsmatrix des gespiegelten Punktes P' bestimmen:
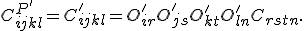
Diese Gleichung wird nun für verschiedene Einträge ausgewertet. So zum Beispiel für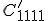 
. Die Transformationsbeziehung lautet:
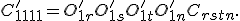
Diese wird für die Indizes r, s, t und n expandiert. Außerdem werden sofort die Einträge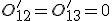 
eingesetzt. Damit erhält man für die Transformationsbeziehung:
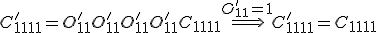
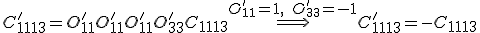
Diese Bedingung ist nur erfüllt wenn 
ist. Hierraus lässt sich folgendes Schema ableiten: Bei einer ungeraden Anzahl des Index 3 in dem Steifigkeitstensor, können die Einträge zu null gesetzt werden. Somit hat die Steifigkeitsmatrix eines monoklinen Materials 13 unabhängige Einträge.
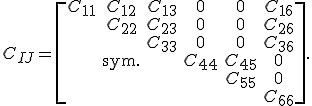
Die Nachgiebigkeitsmatrix lautet somit:
