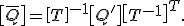Das Vorgehen für die Polartransformation der Steifigkeitsmatrix ist analog zur Transformation der Nachgiebigkeitsmatrix. Der Ausgangspunkt der Berechnung ist das Elastizitätsgesetz im Materialachsensystem. Da der Spannungszustand einer UD-Einzelschicht betrachtet wird und dieser als ebener Spannungszustand angenommen werden kann, wird die reduzierte Steifigkeitsmatrix im Materialachsensystem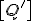 
verwendet:
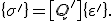(1)
Für die Transformation der Spannungen vom Material- in das Belastungsachsensystem gilt:
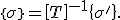(2)
In diese Beziehung wird Gleichung (1) eingesetzt:
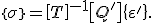(3)
In Gleichung (3) muss noch die Verzerrung im Materialachsensystem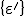 
in das Belastungsachsensystem transformiert werden:
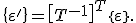(4)
Setzt man Gleichung (4) in Gleichung (3) ein erhält man:
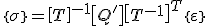(5)
in der man die Definition der reduzierten Steifigkeitsmatrix im Belastungsachsensystem findet:
Die Transformation der reduzierten Steifigkeitsmatrix vom Material- in das Belastungsachsensystem lautet:
 |