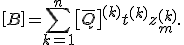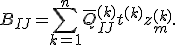Besteht ein asymetrischer Schichtaufbau des Laminats kommt es zu einer Kopplung zwischen Biege- und Zugverformungen. Diese Kopplung wird mit der Koppelsteifigkeitsmatrix beschrieben. Teilt man die Verzerrung in reine axiale Verzerrung 
und einen Anteil aus reiner Biegung 
auf, gilt folglich für die Verzerrungen der Einzelschichten im Belastungsachsensystem 
die kinematische Bedingung:
.
Betrachtet man nun den Kraftfluss erhält man:
.
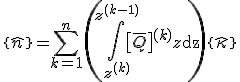Führt man die Integration aus erhält man die Definition der Koppelsteifigkeitsmatrix:
bzw. mit der Definition der Schichtdicke 
sowie der mittleren Schichthöhe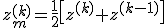 
:
Mit der Superindexschreibweise lautet die Koppelsteifigkeitsmatrix:
Anhand der Koppelsteifigkeitsmatrix lässt sich nun der Vorteil von mittelsymmetrisch geschichteten Laminaten zeigen, denn hier ergibt sich Koppelsteifigkeitsmatrix zur Nullmatrix. Es kommt somit zu keiner Kopplung zwischen Längsverzerrung und Krümmung.
Es soll nun beispielhaft ein mittensymmetrisch geschichtetes Laminat mit vier Schichten betrachtet werden. Dafür berechnet sich die Koppelsteifigkeitsmatrix durch:
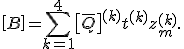
Die Summe wird nun so aufgeteilt, dass in der einen Summe alle Schichten oberhalb und in der anderen Summe alle Schichten unterhalb der Symmetrieebene enthalten sind:
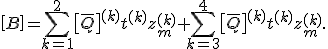
Da die Referenzebene in die Symmetrieebene gelegt wurde gilt für die mittlere Schichthöhe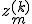 
:
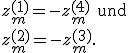
Setzt man diesen Zusammenhang nun in die obige Gleichung ein, wobei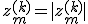 
gilt:
ergibt sich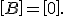 
Die Koppelsteifigkeitsmatrix ist gleich der Nullmatrix, d.h keine Kopplung zwischen Längsverzerrung und Krümmung.