Der Mehrschichtverbund wird mit Hilfe der klassischen Laminattheorie beschrieben, diese wird in den folgenden Abschnitten vorgestellt. Mit dieser 2-D-Kontinuumstheorie wird das globale Verhalten eines Mehrschichtverbundes auf eine Beanspruchung untersucht. Ein Mehrschichtverbund setzt sich dabei aus mehreren Einzelschichten zusammen. Die Einzelschichten können dabei unterschiedliche Faserorientierungen aufweisen, wodurch die gewünschten Materialeigenschaften konfiguriert werden können.

Ziele der klassischen Laminattheorie sind:

• ein Gesamtelastizitätsgesetz für einen Mehrschichtverbund und
• eine schichtenweise Spannungsanalyse.

Bild: Von der Einzelschicht zum Mehrschichtverbund.

Der Zusammenhang zwischen Belastung und Verformung erfolgt mit der Steifigkeitsmatrix. In der unteren Abbildung sind die Einflüsse der Koeffizientenmatrixeinträge bezüglich der Verformung dargestellt.

Bild: Auswirkungen der Koeffizienten und Darstellung der Verformungen [4].

Die Steifigkeitsmatrix setzt sich aus den Untermatrizen zusammen, die im Folgenden hergeleitet werden:

Scheibensteifigkeitsmatrix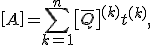
Plattensteifigkeitsmatrix		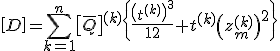und
Koppelsteifigkeitsmatrix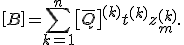