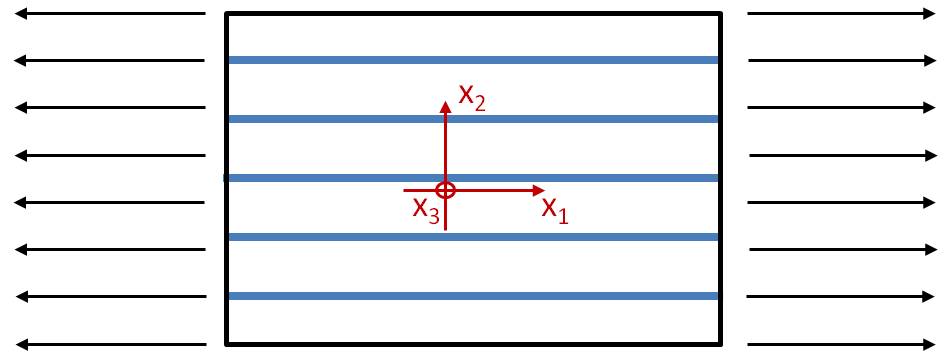
Bisher stimmte das Belastungsachsensystem mit der Faserorientierung überein.
Bild: Draufsicht auf eine UD-Schicht wobei das Material- und Belastungsachsensystem übereinstimmt.
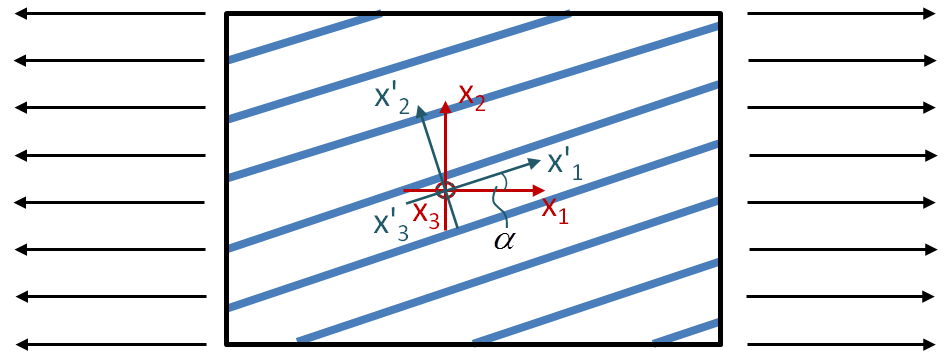
Bei Kompositen befinden sich die Einzelschichten oft mit untschiedlichen zueinander. Das Belastungsachsensystem, auch als globales System bezeichnet, und das Materialachsensystem einer UD-Schicht sind also um einen Winkel 
gedreht.
Bild: Draufsicht auf eine UD-Schicht wobei das Material- und Belastungsachsensystem um einen Winkel
Um nun den Widerstand des Materials im Belastungsachsensystem (x1, x2) zu erhalten, ist eine Transformation notwendig. Die Steifigkeits- bzw. Nachgiebigkeitsmatrix ist somit abhängig von dem Drehwinkel .
Der Faserwinkel 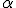ist dabei üblicherweise für eine Einzelschicht im Mehrschichtverbund fest angegeben und kann der Bezeichnung des MSV entnommen werden. Der Faserwinkel wird als positiv bezeichnet, wenn eine mathematisch positive Drehung (also gegen den Uhrzeigersinn) vorliegt. Für eine klare Unterscheidung zwischen dem Belastungsachsensystem und dem Materialachsensystem wird nun eine Umbenennung vorgenommen. Im Folgenden wird das Belastungsachsensystem mit 
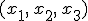und das Materialachsensystem mit 
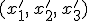bezeichnet. Die Drehmatrix für eine mathematisch positive Drehung lautet:
.
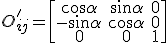Die genaue Vorgehensweise für das Aufstellen einer Drehmatrix ist im Abschnitt Euklidische Transformation dargestellt. Im Folgenden sollen außerdem die Abkürzungen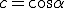 
und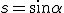 
in den Dreh- und Transformationsmatrizen verwendet werden. Um die Spannungen und Verzerrungen zu transformieren, ist eine zweifache Anwendung der Drehmatrix notwendig. Das Ziel ist es nun die zwei Drehmatrizen zu einer Transformationsmatrix zusammenzufassen. Mit den Transformationsmatrizen für die Spannungs- und Verzerrungstransformation können im Anschluss die Steifigkeits- und Nachgiebigkeitsmatrizen im Belastungsachsensystem bestimmt werden und somit das Elastizitätsgesetz im globalen Belastungsachsensystem aufgestellt werden.