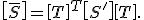Mit den Transformationsmatrizen für die Spannungen und Verzerrungen soll nun das Elastizitätsgesetz im Belastungsachsensystem aufgestellt werden. Bisher ist das Elastizitätsgesetz nur im lokalen, also im Materialachsensystem bekannt und lautet:
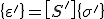. (1)
Die Transformation der Verzerrung vom Materialachsensystem in das globale System ist aus der Verzerrungstransformation bekannt:
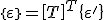. (2)
Nun wird Gleichung (1) in Gleichung (2) eingesetzt:
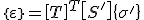. (3)
In Gleichung (3) muss nun noch die Spannung vom Materialachsensystem in das Belastungsachsensystem transformiert werden. Diese Transformation ist bereits im Abschnitt Spannungstransformation gezeigt worden:
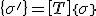. (4)
Es kann jetzt Gleichung (4) in Gleichung (3) eingesetzt werden:
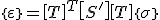. (5)
In Gleichung (5) steht nun die Definition der Nachgiebigkeitsmatrix im Belastungsachsensystem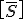 
zu erkennen:
Es muss besonders darauf geachtet werden, dass bei der Nachgiebigkeitsmatrix im Materialachsensystem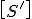 
die Einträge 
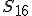und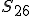 
für transversal-isotrope Materialien gleich Null sind. Die Einträge 
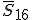und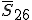 
der Nachgiebigkeitsmatrix im Belastungsachsensystem 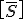sind ungleich Null.
Die Transformation der Nachgiebigkeitsmatrix vom Materialachsensystem in das Belastungsachsensystem lautet:
