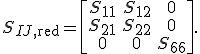Eine Schicht eines Faser-Kunststoff-Verbunds, in welcher alle Fasern in eine einzige Richtung orientiert sind, wird als Unidirektionale Einzelschicht (kurz: UD-ES) bezeichnet. Die Fasern werden dabei als ideal parallel und homogen verteilt angenommen. Die UD-Schicht ist das Grundelement geschichteter Faser-Kunststoff-Verbunde.
In diesem Abschnitt sollen die Steifigkeits- bzw. Nachgiebigkeitsmatrizen für verschiedene Materialsymmetiren hergeleitet werden. Hier wird besonders auf das transversal isotrope Materialverhalten eingegangen, da es die Materialeigenschaften einer UD-ES beschreibt.
Die Steifigkeitsmatrix für ein transversal isotropes Material mit Fasern in x1-Richtung lautet:
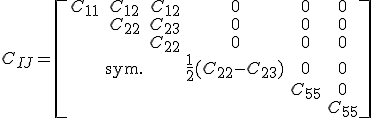
und die Nachgiebigkeitsmatrix lautet:
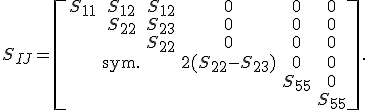
Die Einträge dieser Matrizen werden mit den effektiven Ingenieurskonstanten einer unidirektionalen Einzelschicht besetzt. Die Nachgiebigkeitsmatrix lautet somit:
Wenn der ebene Spannungszustand angenommen werden kann, können die Steifigkeits- und Nachgiebigkeitsmatrizen in reduzierter Form verwendet werden:
 |
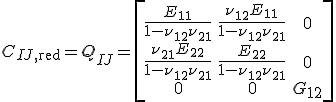und |
|
Für die gedrehte UD-Einzelschicht müssen die Steifigkeits- und Nachgiebigkeitsmatrix transformiert werden. Die transformierte Steifigkeits- und Nachgiebigkeitsmatrix lautet:
 |
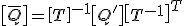und |  |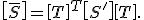
mit der Transformationsmatrix 
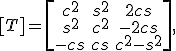
mit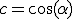 
und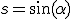 
, wobei 
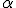der Drehwinkel zwischen Materialachsen- und Belastungsachsensystem ist.