Durch die Betrachtung der Materialsymmetrien ist die Struktur der Steifigkeitsmatrix bekannt. Es ist nun von Interesse die genauen Einträge durch die Ingenieurkonstanten auszudrücken. Dafür sind zwei Arten von gedanklichen "Experimenten" notwendig:
(a) einachsige Zugversuche und
(b) Scherversuche.
Es wird im Folgenden ein transversal-isotropes Material betrachtet, welches eine Rotationssymmetrie bezüglich der x1-Achse aufweist. Das Materialgesetzt lautet:
Hierbei wurde das Materialgesetz mit der Nachgiebigkeitsmatix 
verwendet, da in den gedanklichen "Experimenten" die Spannungen 
vorgegeben werden.
(1)
Mit Hilfe der gedanklichen "Experimente" (zwei Zugversuche, ein Scherversuch) können die Einträge der Nachgiebigkeitsmatrix bestimmt werden.
Die Steifigkeitsmatrix ist die Inverse dieser Matrix.
Bei der Berechnung der Einträge der Nachgiebigkeitsmatrix ist zu beachten, dass auch die Querkontraktionzahl richtungsabhängig ist:
Aufgrund der Symmetrie der Nachgiebigkeitsmatrix sind die Einträge 
und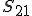 
gleich. Somit entspricht das Verhältnis der Querkontraktionszahlen dem Verhältnis der Elastiztätsmodule:
