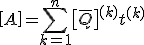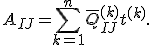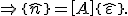Scheiben werden nur durch Kräfte in der Ebene belastet. Für die Herleitung der Scheibensteifigkeitsmatrix werden wieder die bekannten drei Schritte der Elastostatik angewendet:
(i) geometrische Beziehungen/ Kinematik,
(ii) Gleichgewicht/ Kräftegleichgewicht und
(iii) Werkstoffgesetz.
(i) Kinematik
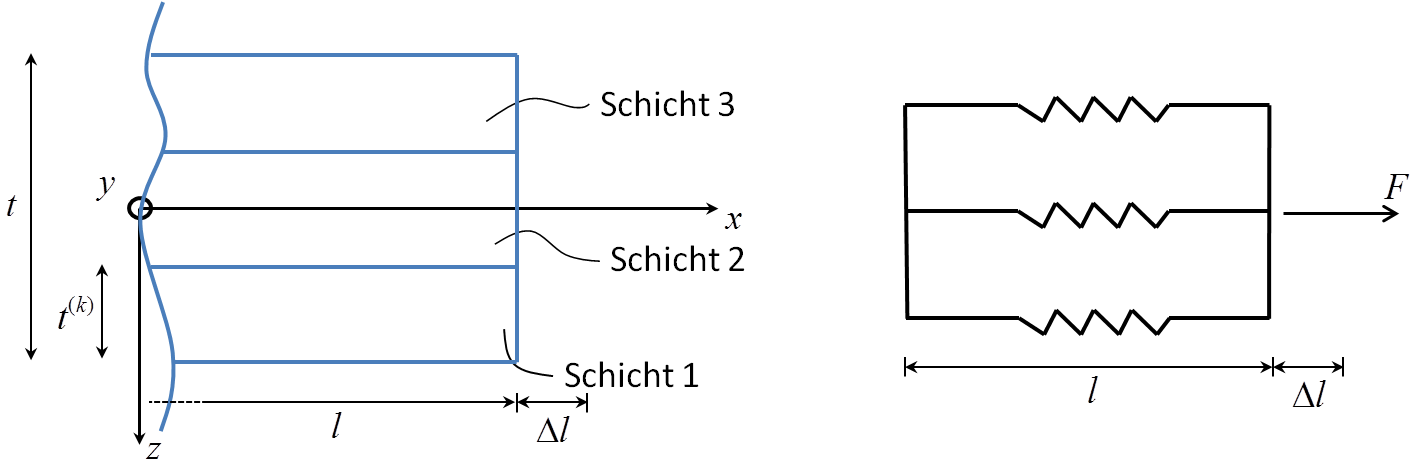
Ein Mehrschichtverbund kann in der Ebene als eine Federparallelschaltung modelliert werden. Die einzelnen Federsteifigkeiten werden durch die Steifigkeiten der Einzelschichten bezogen auf das Belastungsachsensystem dargestellt. Dies ist in der unteren Abbildung exemplarisch für ein Mehrschichtverbund mit drei Einzelschichten dargestellt.
Bild: Exemplarische Darstellung eines Mehrschichtverbunds mit drei Einzelschichten für die Herleitung der Scheibensteifigkeitsmatrix.
Durch die Parallelschaltung ist die Gesamtdehnung, also die Dehnung des Mehrschichtverbunds, identisch mit der Dehnung der Einzelfedern und somit der Dehnung der Einzelschichten.
| MSV | Einzelschicht | |
| x-Richtung | 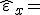 |
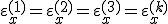 |
| y-Richtung | 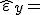 |
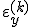 |
| Scherung | 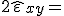 |
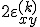 |
(1)
(ii) Gleichgewicht
Bei einer Federparallelschaltung entspricht die außenanliegende Kraft der Summe der Kräfte in den Einzelschichten.
| MSV | Einzelschicht | |
| x-Richtung | 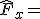 |
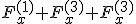 |
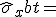 |
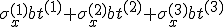 |
|
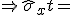 |
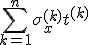 |
|
| y-Richtung | 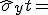 |
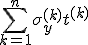 |
| Scherung | 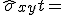 |
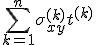 |
(2)
(iii) Werkstoffgesetz der Einzelschicht im Belastungsachsensystem
Das Werkstoffgesetz einer Einzelschicht im Belastungsachsensystem ist bereits bekannt:
(3)
Um nun das Elastizitätsgesetz des Mehrschichtverbunds zu erhalten wird zunächst Gleichung (3) in Gleichung (2) eingesetzt:
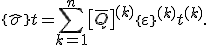
Wird nun die Dehnungen aus Gleichung (1) verwendet erhält man:
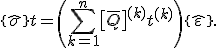
Der Ausdruck in der Klammer ist die Definition der Scheibensteifigkeitsmatrix 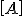 :
:
bzw.
Das Gesamtelastizitätsgesetz eines Mehrschichtverbundes als Scheibenelement lautet nun mit der Definition des Kraftflusses 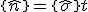 :
: