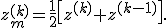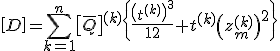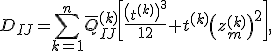Für die Betrachtung des Laminats als Plattenelement wird reine Biegung vorausgesetzt. Es gelten die Annahmen der Krichhoffschen Plattentheorie. Für Laminate ist speziell hinzuzufügen:
- die Schichten sind eben und weisen eine konstante Dicke auf,
- die einzelnen Schichten sind perfekt miteinander verklebt; es tritt kein Gleiten zwischen den Einzelschichten auf,
- keine Klebschichten zwischen den einzelnen Schichten.
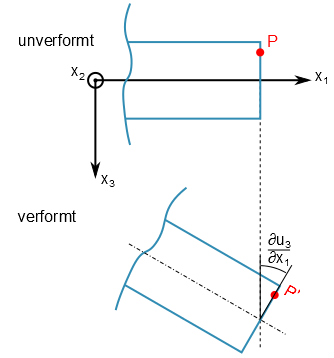
Die Kirchhoffsche Plattentheorie fordert dass Plattenquerschnitte auch nach Verformung senkrecht und rechtwinklig auf der Mittelebene stehen. Dabei setzen sich die Verzerrungen aus einem axialen Verschiebungsanteil und einem Anteil aus reiner Biegung zusammen.
Bild: Zusammensetzung der Verzerrungen unter Annahme der Kirchhoff Hypothese.
Für den Anteil aus reiner Biegung gilt:
.
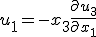Mit der Definition der Verzerrung:
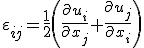
folgt nun
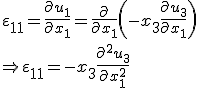
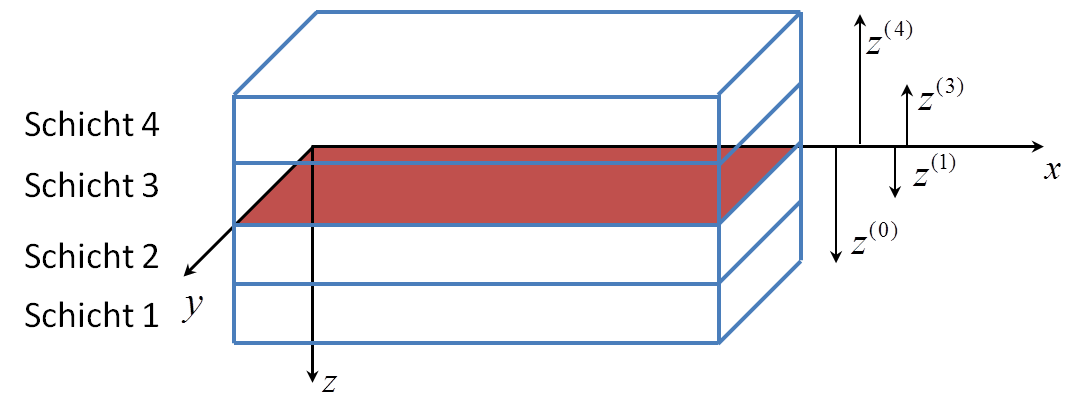
Um den Anteil aus reiner Biegung zu berechnen, ist die Definition einer Bezugsfläche notwendig. Diese wird bei einer mittelsymmetrischer Schichtung für eine vereinfachte Rechnung in die Symmetrieebene gelegt.
Bild: Wahl der Bezugsebene.
Für das weitere Vorgehen zur Bestimmung der Plattensteifigkeitsmatrix benötigt man wieder:
(i) die Kinematik,
(ii) das Gleichgewicht und
(iii) das Werkstoffgesetz.
Aufgrund der idealen Verklebung der Einzelschichten gilt für die Kinematik, dass die Verzerrung des Mehrschichtsverbundes mit den Verzerrungen der Einzelschichten übereinstimmen:
.
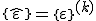Mit Hilfe der Definition der Krümmungen ergibt sich:
,
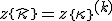wobei für die Krümmung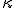 
folgendes gilt:
.
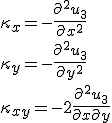Die Gleichgewichtsbedingung wird über die Momentenäquivalenz aufgestellt. Dabei ist das außen, am Mehrschichtverbund anliegende Moment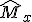 
identisch mit der Summe der Momente der Einzelschichten. Das außen anliegende Moment berechnet sich durch das Integral der äußeren Spannung über die Gesamtdicke, wobei 
die Laminatbreite definiert:
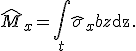
Das Moment in einer Einzelschicht berechnet sich durch das Integral der Spannung über die Schichtdicke. Für die Summe der Momente der Einzelschichten gilt somit:
.
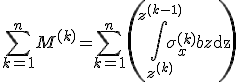Teilt man nun das außen anliegende Moment und die Summe der Momente der Einzelschichten durch die Breite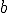 
erhhält man den sogenannten Momentenfluss 
:
.
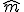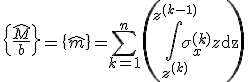Das Werkstoffgesetz ist bisher nur für die Einzelschicht bekannt und lautet mit der reduzierten Steifigkeitsmatrix der Einzelschicht im Belastungsachsensystem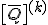 
:
.
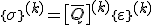Nun wird das Werkstoffgesetz in die Momentenäquivalenz eingesetzt:
.
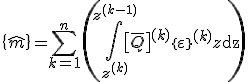Mit der kinematischen Bedingung der reinen Biegung:
folgt daraus:
.
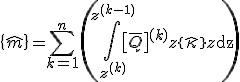Wird die Integration ausgeführt erhält man:
bzw.
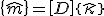
mit der Definition der Plattensteifigkeitsmatrix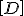 
:
Für rechteckige Querschitte lässt sich diese Definition vereinfachen:
bzw.
mit der Schichtdicke 
und der mittleren Schichthöhe 