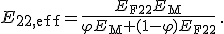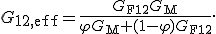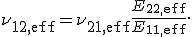Bild: Veranschaulichung des Vorgehens für die Berechnung der effektiven Ingenieurskonstanten in Faserquerrichtung.
Nun wird die Gleichgewichtsbedingung, Kinematik und das Werkstoffgesetz aufgestellt.
1. Gleichgewichtsbedingung
Es wird ein Kräftegleichgewicht in Faserquerrichtung aufgestellt. Aufgrund der Idealisierung des Systems als Reihenschaltung von Federn ist die angreifende Kraft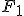 
gleich der resultierenden Kraft in der Faser 
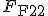und der resultierenden Kraft in der Matrix 
.
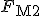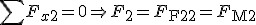
Aufgrund der identischen Kraftangriffsflächen ergibt sich für die Spannungen:
(1)
2. Kinematik
Bei Reihenschaltung von Federn ist die Gesamtauslenkung die Summe der Auslenkung der einzelnen Federn:
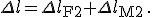
Über Definition der Verzerrung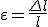 
kann diese Gleichung umgeschrieben zu:
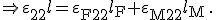(2)
3. Werkstoffgesetz
Das Werkstoffgesetz für den eindimensionalen Fall (Hooke'sches Gesetz) wird jeweils für das homogenisierte Gesamtsystem, die Faser und die Matrix aufgestellt:
| homogenisiertes Gesamtsystem |  |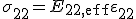
(3) |
| Faser |  |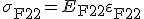
(4) |
| Matrix |  |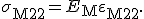
(5) |
Im Folgenden sollen die Verzerrungen mit dem relativen Faservolumenanteil dargestellt werden. Hierfür wird die Definition des relativen Faservolumenanteils über die Größe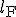 
verwendet. Teilt man also Gleichung (2) durch die Ausgangslänge 
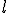so findet sich diese Definition wieder:
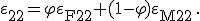(6)
Nun werden die Verzerrungen der Faser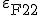 
und der Matrix 
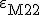in Gleichung (6) durch das Materialgesetz aus Gleichung (4) und (5) ersetzt:
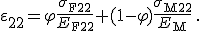(7)
Durch die Gleichheit der Spannung aus Gleichung (1) kann man die Faser- und Matrixspannung durch die allgemeine Spannung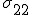 
ersetzen und diese wiederum ausklammern:
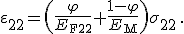(8)
Dividiert man nun durch den Faktor von 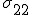ergibt sich:
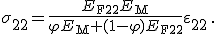(9)
Vergleicht man nun noch Gleichung (9) mit dem Stoffgesetz aus Gleichung (3) erhält man daraus das effektive E-Modul in Faserquerrichtung:
Das Vorgehen für das Schubmodul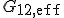 
ist analog und liefert:
Die Querkontraktionszahl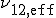 
berechnet sich aus dem effektivem E-Modul in Faserlängsrichtung 
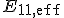und dem effektivem E-Modul in Faserquerrichtung 
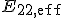, sowie der Querkontraktionszahl in Faslängsrichtung 
:
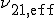